FAVOR TMと物体適合座標系
複雑な幾何形状領域をモデル化するために面積/体積占有率を測定する FAVOR TM法の簡潔さは、非常に魅力的です。しかし、有限要素法やBFC (body-fitted coordinate: 物体適合座標)法で採用されているような変形格子と比べた場合、精度の点で競り合うことはできるのでしょうか。これらの手法を比較することにより、この2つのアプローチの機能の違いはほんのわずかであることがわかります。
固体の境界が存在しない場合、形状が異なるコントロールボリュームの格子の間には、根本的な違いはほとんどありません。手法によって、ユーザが保存する必要のある情報が多い場合(ノードの場所、さまざまな幾何形状要素など)や、要素の歪みの量によって精度レベルが異なる場合があります。しかし、どの場合も、根底にある考え方は、格子内の要素ごとに流体の力やフラックスが計算される離散近似です。
これは、幾何形状に適合するように構築できるという変形可能な格子のメリットとして取り上げられることの多い、障害物境界の問題です。この柔軟性には、2つの結果が伴います。1つは、これらの格子は、汎用目的では非構造でなければならないということです。構造格子の場合、ほんの少し歪みを加えただけで、要素が裏返しになるからです。もう1つは、要素の歪みによって、正確な数値近似を構築することがさらに困難になることです。
構造 FAVOR TM格子と非構造格子
FAVOR TMの概念は、長方形要素や歪みのある要素から成る格子を含めて、また、構造格子か非構造格子かにかかわらず、あらゆるタイプの格子と関連させて使用できます。中でも、構造格子が最適です。構造格子は簡単に生成でき、隣接要素のインデックスがわかっているからです。長方形の格子要素を使用すると、 FAVOR TM法で使用されている要素の面積占有率や体積占有率を簡単に計算できます。
長方形の構造格子は、簡単に生成できるため、 FAVOR TM法ではこれを選択するのが当然のようになっています。ただし、FAVORTM法には開いた格子領域と閉じた格子領域の指定が潜在するため、一種の非構造計算環境となります。これは、開いた体積の大きさが有限である要素のみが実際に計算され、その結果、非構造格子の計算と類似した計算になるからです。
本当の非構造格子との類似は完全ではありません。たとえば、 FAVOR TM法では、ブロックされているかどうかにかかわらず、すべての要素のストレージが必要ですが、非構造格子には隣接リストのストレージが必要です。どの要素が隣接しているかを自動的に知ることができる代わりに、すべての要素を保存しなければなりません。もちろん、流体を囲む固体領域で熱伝導が計算される場合は、ブロックされている要素はいずれにしても保持する必要があります。
長方形の構造格子に関連するデメリットの1つは、局所化された領域で変形させて解像度を上げることができないことです。格子線は、特定の領域で解像度を上げるために細かく作成できますが、こうした格子線はその後、格子全体に広がります。その結果、1つの格子内の要素の数が大きくなる場合があります。このデメリットを相殺するのが、格子生成の簡単さです。また、境界で結合された複数の格子ブロックを導入することにより、格子セルの数を大きく増やすことなく、局所的な解像度を上げられる可能性もあります。
FAVOR TM法は、非構造格子と類似した特性を持つと見られていますが、非構造の物体適合格子や有限要素格子の構築に関連するオーバーヘッドはありません。格子生成には時間と労力を大量に投資しなければならない場合が多いため、この作業が不要になることで、FAVORTMは非常に望ましい選択肢となっています。
FAVORTMの要素とBFCの要素
変形格子の2番目の問題は、境界の固体表面への適合に変形を使用できることです。これを行うには、表面に最も近い要素のノードを表面に移動します。これに対して、 FAVOR TM法では、表面が要素に切り込むことができ、その位置は、要素の端を移動することによってではなく、固体で覆われていない要素の表面積占有率と体積占有率によって記録されます。
ここで見ていただきたいのは、固体境界を定義するための面積/体積占有率の手法の数値近似の結果が、変形(BFC)格子手法と同じであることです。
FAVOR TM法に関して理解するべき最も重要な点は、流体力学の量の近似は、要素の開いている領域に限られることです。この制限により、要素の面積/体積占有率は、因数として、離散近似に直接導入されます。たとえば、要素から要素への量のフラックスは、乗数として、流れに対して開いているフラックス境界の面積占有率を持っています。
このように、 FAVOR TMとBFCはいずれも、同じ面積を使用する要素の面を通過するフラックスを計算します。 FAVOR TMでは、面積は元の要素表面積に対する割合として保存されます。BFC法では、面積は、面を定義するノードの座標から計算されます。多くの場合は保存もされるため、再計算の必要はありません。
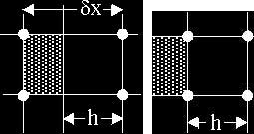
図1: 左はFAVOR<sup>TM</sup>のブロックセル(a)、右はBFCのセル(b)。網掛け部分が固体領域。
FAVOR TMでは、セルの開いた部分の幅は、開いた体積占有率と元のセル幅の積に等しくなります。この積が、 FAVOR TMで横方向の差分近似に使用されます。またこれは、変形されたセルの幅hと同じです。
縦方向、たとえば要素の上面と交差(図1の固体境界と平行)する方向で差を計算する場合、 FAVOR TM法の近似には、上面の面積占有率を体積占有率で割った比率が関係します。この比率の値は1です。これは、固体境界によって、体積と同様に、同じ面積占有率が横方向にブロックされるからです。これにより、ここでも、近似はBFCセルと同様になります。このように、FAVORTMのセルとBFCのセルでは、差分近似を行う際に使用する有効セル幅に違いはありません。
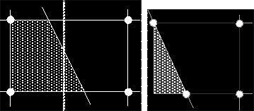
図2: 左はFAVOR<sup>TM</sup>のセル(a.)、右はBFCのセル(b.)。網掛け部分が固体領域。
まとめ
BFC格子の構築が難しいことはよく知られており、「自動」格子生成機能の開発には多大な努力が注がれてきました。また、最高クラスの格子生成機能を使用したとしても、有効かつ適切な機能を果たす格子を作り上げるには、かなりの時間がかかることも、よく知られています。
FAVOR TMの格子は、単純な長方形の構造であるため、非常に簡単に生成できます。格子内に配置する障害物を定義するために面積占有率や体積占有率を計算する必要がありますが、こうした計算はよく定義されており、単純なアルゴリズムを使用して簡単に自動化できます。
格子生成の手法としてBFCではなく FAVOR TMを選択しても、数値的精度が犠牲になることはありません。この2つのアプローチは、境界表面の近似方法が異なっているだけです。
最後に、 FAVOR TM法で使用されている、構造化され、変動が滑らかで、厳密に直交する格子に固有の数多くのメリットは、見過ごすべきではありません。これらのメリットと、多孔質媒体(面積/体積占有率領域のもう1つの例)を自動的に表現する機能は、 FAVOR TM法がFLOW-3Dの基盤として選ばれたもう1つの理由です。