ラグランジュ粒子
十分に定義された界面によって隔てられた、随時大きな変形が発生するさまざまな物質の挙動をシミュレーションする数値流体力学のプログラムを想像できますか。また、このプログラムが衝撃波を捉え、希薄化、すべり表面、その他の非線形の流体力学現象を追跡することを想像できますか。
そのようなプログラムの開発は、気が遠くなるような作業です。このようなプログラムが1955年に稼働していたと言ったら、驚くかもしれません。コンピュータグラフィックスや機械式ペンプロッタが実用化されるずっと以前のことであり、Fortranのような高水準プログラミング言語さえもまだ一般的になっていなかった頃のことです。Fortran、つまりFormula Translation Systemは、1954年にIBMによって提唱されました。これらの素晴らしい機能を持つプログラムはPIC (Particle-In-Cell)法と言い、ロスアラモス国立研究所(Los Alamos National Laboratory)のFrancis H. Harlow氏によって考案されました(F.H. Harlow、『A Machine Calculation Method for Hydrodynamic Problems』、Los Alamos Scientific Laboratory report LAMS-1956、Nov. 1955)。
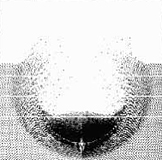
図1: 直径2cmの鉄球が
超音速でアルミニウム板に
衝突した場合のPIC計算
それなのになぜ、PIC法は連続流体力学にもっと広く使用されていないのでしょうか。たとえば、この手法に基づいている市販のCFDプログラムはありません。PIC法は圧縮性流れに最適である一方、ほとんどの市販アプリケーションでは非圧縮性流体の状況を取り扱っているということが言えるかもしれません。
PIC法がより賢明に使用されていない理由が他にも2つありますが、それらはラグランジュ粒子の離散性に関連しています。こうした離散化特性およびその結果こそが、本書の主題です。明らかな特性の1つは、粒子の数の変化によって、数値の有限変化が発生する場合があることです。もう1つの特性は、それほど明確ではなく、流体のある基本的な特性に関連しています。この特性により、質量の中心(離散化)位置を追跡するだけでは流体要素を追跡するのが困難になっているのです。
離散化の問題
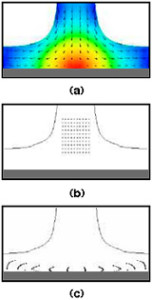
図2:(a) 噴流が壁に衝突したときの流れ、(b) 粒子の初期分布、(c) その後の、垂直方向に圧縮し、水平方向に分散する粒子分布
経験から、PIC法は、セルあたりの粒子数が16個以上(2次元の場合は4×4配列、3次元の場合はセルあたり64個の粒子)である場合に最適に機能することがわかっています。より大きい変動を許容できる場合(または、CFDの初期に多かった状況として、コンピューティング資源の問題により、大きい数値を使用できない場合)は、使用する粒子数はもっと少なくてもかまいません。
粒子の初期配置が規則的ではなく不規則だった場合に良い結果が得られることも、経験によってわかっています。その理由は簡単に確認できます。粒子が規則的な4×4の配列でx-y空間に並んでいるとします。流れがx方向のみの場合、4個の粒子から成る列が、セルからセルへ同時に移動するため、セルの値が大きく変化する結果となります。ただし、空間に粒子が不規則に配置されている場合は、セルの境界を通過する粒子は1回につき1個だけになる可能性が高いため、セルの値の離散変化は最小限になります。
最近になって、粒子がセルからセルへ移動する際の離散変化の影響を軽減するために、別のアプローチが使用されてきました。これは「平滑粒子流体力学」法であり、粒子は、同時に複数の格子セルと重なる可能性のある有限の体積を持ちます。粒子がセル境界に近づくと、その体積は、元のセルから隣のセルへ、連続してスイープします。
要素の歪みの問題
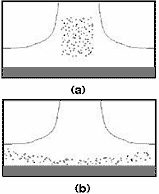
図3:粒子の初期分布が不規則であることを除いて図2 B-Cと同様
このタイプの変形は、流体要素の物質が局所化されたままにはならず、質量の中心に従うラグランジュ粒子では要素を十分に表現できなくなることを意味します。計算法では、要素の歪みがさまざまな問題につながる場合があります。最も一般的な問題の1つは、粒子は均一な分布を保持するのではなく、場所によって1個所にまとまったり、散り散りになったりする傾向があるということです。
こうした過程の簡単な例は、よどみ点で発生します。図2は、液体噴流が壁に衝突し、衝撃の中心にあるよどみ点の両側に流れるときに、規則正しい粒子配列に何が起きるかを示しています。粒子は、壁に対して垂直方向にまとまり、同時に壁に沿って外側に離れて行くように移動します。
初期分布の粒子が不規則な場合、こうした変形過程は大幅に減少します。図3を参照してください。あいにく、不規則な分布でも、この問題を完全に排除することはできません。剥離点や、せん断力が強い領域など、その他の状況では、粒子を不規則にしても、粒子の均等な分布を維持するには十分ではありません。
膨張領域に粒子を追加したり、収束領域で粒子を除去したりするために、数多くの手法を使用できます。また、連続再パーティション法を使用して、より均等になるように粒子を再配置することもできます。ただし、こ
うした操作では、オイラー計算法と事実上同等の局所的平滑化が行われ、粒子の最も優れた特徴の1つである独自性が失われます。
その他の注意点
流れの剥離領域が問題の原因となる理由は、粒子の均一な分布を維持することが困難なことだけでなく、剥離点近くの流れに湾曲があることです。
流れの湾曲がなぜ問題になるのかを理解するために、流体の剛体回転について考えます。そのような流れの中に配置されたラグランジュ粒子は、回転軸を中心として円を描くように動きます。実際には、このようなことはめったに起こりません。粒子を導入する際は、多くの場合、速度の1次式を使用して粒子の位置を前進させるからです。たとえば、タイムステップn+1における粒子のx位置はxn+1=xn+dtUと計算されます。ここで、dtはタイムステップサイズ、Uは粒子の位置における流れの速度のx成分です。
この式は、速度の1次式であり、円の接線方向に粒子を動かします。その結果、粒子は、接線に沿って移動されたときに、わずかに大きい半径に移動します。十分な数のタイムステップの後に、粒子は外側に投げられているように見えます。これは、数値的遠心効果の一種です。
このタイプの挙動の唯一の修正方法は、流れに湾曲があるときに感知して、2次式を使用して粒子の新しい位置を計算することです。
拡散過程は、ランダムウォークの一種であるモンテカルロモデルを使用して、粒子法に簡単に含めることができます。1つの手法は、粒子が外向きに拡散する物質の点源であると仮定することです。短い時間(dt)、拡散はガウス分布を持っている(点源の拡散方程式の解を持っている)と表すことができます。粒子は細分化できないため、この分布は代わりに確率分布として処理されます。その後、粒子は、dtという時間間隔で最も確率の高い位置に移動されます。この確率分布では、乱数発生器を使用して位置が選択されます。これは、十分な試行を実施すれば、粒子が与えられた位置に達する回数はガウス分布に比例するという考え方です。

図4:円筒状の水柱(a)が崩れて円形の凸部に当たってしぶきを上げる(b)様子の計算。粒子の指状の部分が特にリアルに見えるが、粒子は計算には使用されていない。
図4は、円柱(左の輪郭部分)が崩れることから始まって、円筒形の凸部に当たってしぶきを上げる液体の流れをMACのように計算した場合を示しています。しぶき上部の、マーカ粒子の小さい指状の部分が、特にリアルに見えます。たまたま、この計算は、VOF (Volume-of-Fluid)法を使用して行われ、ラグランジュ粒子には計算上の役割はありませんでした。図の中の粒子は、グラフィック表示のためだけに計算に含まれました。
この例は、離散化された粒子が正確であることの強力な根拠と思われるもの、つまり、局所的詳細を捉える能力が、この場合は主に視覚効果であることを示しています。これは、純粋なセル平均の量から力学が計算されたためです。
ラグランジュ粒子は、特に、分散を最小限にしなければならない少量の物質を追跡する場合に、非常に便利な計算ツールです。ただし、連続媒体の離散モデルとして粒子を使用する場合は、いくつか制限事項があることを覚えておく必要があります。この意味で、粒子は他の離散計算法と何ら違いはありません。ラグランジュ粒子を使用する際に注意が必要な問題のいくつかを、本書の中で少しでも示すことができたら幸いです。