無条件数値安定性の確認
時間発展方程式を解く際に使用する陽的(時間が進行する)有限差分近似が、時間増分のサイズの極限に支配されることは、よく知られています。このタイプの近似では、すべての従属変数の値の時間が、連続する短い時間間隔で進行すると仮定されています。ステップnまでのすべてのステップにおける変数値がわかっていれば、それらを使用して変数の変化率を推定できます。これにより、ステップn+1における従属変数の値を推定できます。これはδtという短い時間が経過した後に相当し、tn+1=tn + δtとなります。
このタイプの近似で小さい数値δtが必要になったのは、従属変数の変化率が、通常は、該当する変数と、空間内でその変数のすぐ隣にある変数の値の差を基準として評価されるからです。タイムステップサイズが拡大する場合、変数は、すぐ隣の変数だけでなく、遠く離れた場所にある値の影響も受けると予測されます。この意味で、精度を確保するために、時間進行のサイズδtに極限を設ける必要があります。実際に、この極限は、計算の安定性を確保するためにも必要です。
陰解法と陽解法
陽的有限差分方程式は、解の時間を進行させるための指示がわかりやすいため、簡単に使用できますが、タイムステップサイズδtを制限して計算を安定させる必要があるため、計算時間が長くなる可能性があります。この制限を克服するために、面倒なタイムステップ制限が不要な陰的有限差分法を使用することが望ましい場合もあります。基本的な考え方は、ある変数の変化率の近似に、進行した時間レベルn+1における変数の値を含めるというものです。計算対象となるレベルn+1の値が、これらの同じ値に依存するようになるため、この差分方程式は陰的と言います。
陰解法では、時間発展の方程式を解くことが、より難しくなります。たとえば、多くの場合、反復解法を使用する必要があります。反復法は、陽的な時間進行(サブタイムステップを使用)と同じように見える場合もありますが、うまく機能した場合、急速に過渡現象を減衰させ、比較的少ない反復回数で、進行したタイムステップn+1における収束解に達するため、陽解法のような精度は期待できません。
安定性の簡単なテスト
陰的有限差分近似が無条件に安定しているかどうかを確認するために使用できる、非常に簡単な手法があります。つまり、どんなに大きいタイムステップサイズを使用しても、数値的な不安定に関連する無意味な結果にはならないかどうかをテストします。手順は、差分方程式を、方程式に出現する最大のδtの累乗で割るというものです。次に、δtの極限を取り、無限にします。方程式のほとんどの項がゼロになります。残った式に、解を求める変数のn+1以外の値が含まれている場合は、δtに何らかの極限があり、方程式を無条件に安定させることはできません。
一方で、δtが無限になった後に残った式で変数のn+1値を求めることができる場合、これは無条件の安定性を意味します。もちろん、無限のδtから求められた値は、現実的ではない場合があります。たとえば、負の温度は、無限δtの極限で陰的差分方程式の解となり得ますが、負の温度は物理的意味を成さないため、良い解ではありません。
δt極限の例
δt極限テストの簡単な例として、次の1次元熱伝導方程式について考えます。
![]()
長さδxの要素の均一格子上の複合陽的/陰的差分近似は次のとおりです。
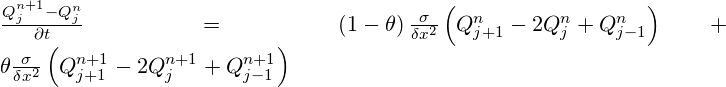
θは、陽陰の混合に重み付けします。θ=0は純粋に陽的な近似を提供し、θ=1は完全に陰的な近似を提供します。θ=1/2の値は、時間および空間が2次精度である近似を提供します。
タイムステップ極限テスト
δtが無限になると、方程式の左辺がゼロになります。右辺は、θがゼロ以外の場合、つまり、近似に何らかの陰的要素がある場合にのみ、Qn+1の式を与えます。このことから、単純な陽的近似には極限のδtが必要であること、また、これが無条件に安定してはいないことがわかります。一方で、陰的近似では、Qn+1の解が常に与えられるため、これは無条件に安定しています。しかし、これで良い解が得られるでしょうか。
この単純なケースでは、境界値Q0およびQJ、0 < j < Jに関して、左辺がゼロの場合に、差分方程式の厳密解を書くことができます。
![]()
θの値が1以外の場合は、末項がQn+1に対して負の値になる可能性があります。θ=1のとき、負の値になる可能性はなく、実際の結果は、正しい漸近解、つまり、境界値を結合する線形温度プロファイルになります。
無限のδt極限は、無条件の安定性の有無を示すだけでなく、大きなタイムステップにおける解の質に関して便利な情報をもたらすこともできる簡単な手法です。