数値不安定性

数値不安定性

偏微分方程式の多くの数値近似は、不安定な計算結果が生じるため不安定です。計算安定性の問題は、「数値流体力学モデルの基礎」シリーズの直前の2項、すなわち計算安定性とヒューリスティック解析で議論されています。この項では、ナビエストークス方程式に関連する一般的な数値不安定性の理解につながるシンプルな機械的モデルについて説明します。このシンプルなモデルは特に、粘性応力、表面張力、弾性などの流体力学的な力から生じる不安定性に適用されます。シンプルなモデルによって得られる安定性条件は、特定の数値近似に依存しませんが、代わりに質量と力に関する一般的な検討事項のみを含みます。

モデルシステム

Figure 1. Model System

図1. モデルシステム

図1に示すように、2つの剛体壁の間に位置し、それらの壁にばねで接続されている質量Mを想定します。ブロックに作用するばね力がばねの長さの変化に比例するフックの法則をこれらのばねが満たすと仮定した場合、水平方向にのみ移動するブロックの運動方程式は下記のようになります。

(1) \displaystyle M\frac{\partial U}{\partial t}=-2k\left( X-{{X}^{0}} \right)

記号X0はブロックの初期x位置を表し、記号Mはブロックの質量を表します。初期状態ではX=X0であり、ブロックは静止しており、U=0です。ここで、時間t=0で速度U0を指定することによって、ブロックに摂動を与えると想定します。微小時間間隔δtの後、ブロックは位置X1=X0+U0δtに移動し、式1の単純な離散化によって時間間隔の最後における速度は下式のように表現されます。

(2) \displaystyle M\left( \frac{{{U}^{1}}-{{U}^{0}}}{\delta t} \right)=-2k\left( {{X}^{1}}-{{X}^{0}} \right)

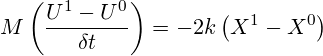
X1を値X0+U0 δtに置換して整理すると、新しい速度U1の式が得られます。

(3) \displaystyle {{U}^{1}}={{U}^{0}}\left( 1-2\frac{k\delta {{t}^{2}}}{M} \right)

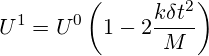
これは再帰式であり、連続する各時間ステップについて、その時間ステップの最後での速度が、前の時間ステップの速度値に式3の括弧内の量を乗算したものに等しくなるため、n時間ステップ後は下記のようになります。

(4) \displaystyle {{U}^{n}}={{U}^{n-1}}\left( 1-2\frac{k\delta {{t}^{2}}}{M} \right)={{U}^{0}}{{\left( 1-2\frac{k\delta {{t}^{2}}}{M} \right)}^{n}}

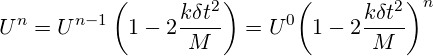
式4の括弧内の量の上付き文字が時間水準指標ではなく指数であることに注意してください。ただし、この例では指数の値と時間水準指標は同じです。式4より、括弧内の量が1.0よりも大きな絶対値を持つ場合、速度Unはnの増加とともに指数的に増大することが分かります。そのため、このモデルシステムでの速度の指数的増大を防ぐためには、下記の不等式を満たすように時間ステップサイズを制限することが必要です。

(5) \displaystyle \frac{k\delta {{t}^{2}}}{M}\le 1

式5の左辺が1よりも大きい場合、速度Unは大きさが指数的に増大しつつ、連続する時間ステップで正の値と負の値の間を振動することになります。

この挙動は古典的な数値不安定性の特徴です。この例では、不等式を満たすためにδtを十分に小さく保つことによって、不安定性を防ぐことが可能であると式5によって示されています。一般に、数値不安定性が発生し、連続する時間ステップで増大する正と負の値の特徴が表れた場合は、時間ステップサイズを小さくすることによって対処することが可能です。

このシンプルな機械的モデルをさらに検討すると、不安定性が初期作用に対する過剰反応に起因していることが式4から分かります。つまり、時間ステップサイズが大きい場合、式4では反対方向の、大きさが増大した新しい速度が予測されます。この過剰速度が、今度は次の時間ステップの開始条件になり、速度の大きさの指数的な増大につながります。

式5の安定性条件は、陽的定式化に基づいています。これは、質量の現在の応答が以前の変位によって表現されることを意味します。質量の現在の応答が後続の位置に基づく陰的定式化(つまり、式2でX1の代わりにX2を使用)では、無条件に安定だと考えられますが、未知の最終位置X2が既知であることが必要になります。大半の方程式の場合、陰的解法では反復解析が必要になるため、反復解析に必要な追加の計算量は、安定性条件をなくすために支払うべき代償になります。

ナビエストークス方程式への適用

上記の機械的モデルの数値不安定性を利用してナビエストークス方程式で生じる可能性がある不安定性を理解するため、図2に示すように、2個の要素を分ける境界上の速度に摂動が与えられている、オイラー計算格子による2個の要素を想定します。

Figure 2. Grid Model

図2. 格子モデル

簡単のために、実線によって輪郭が描かれている要素が同一サイズの立方体であるとし、ベクトルがx方向の速度を表しているものと考えます。両要素の中央(つまりyx平面)にある破線によって、速度Uに割り当てられている要素の部分体積の範囲が定義されます。部分体積内にある流量の全質量は、機械的モデルにおける質量Mと相関があります。速度Uによって要素間の流体が動かされた場合、機械的モデルのばねとまったく同様に、速度に対抗して作用する力を発生することによって要素は応答します。これらの力は、流体、粘性応力、表面張力(流体と質量Mの範囲内に流体界面がある場合)またはその他の力による圧縮または引張のために発生する可能性があります。各例で適切な剛性係数kを特定することによって、図2に示すような格子内で陽的数値近似を使用する場合、式5を使用してこの物理過程に対する安定性基準に到達することが可能です。

この類似性をどのように適用できるかについての例を、以下の各項で示します。各例において、部分体積内の流体の質量Mは下式によって与えられます。

(6) \displaystyle M=\rho \delta x\delta y\delta z,

ここで、ρは流体の密度であり、要素の寸法はδx、δyおよびδzです。

圧縮性流体

剛性係数kを求めるには、kが加えられた摂動に抵抗するために生み出される力の尺度であることを思い出してください。圧縮性流体の場合、この力は流体圧力の変化に関連しています。これは、熱力学的関係dp=c2dρによる流体密度の変化によるものです。ここで、cは流体中の音速です。要素間の境界を越えて移動した流体の質量はρUδt*δyδzであり、質量を受け取る要素内での密度変化は、この質量を要素の体積で除算したdρ=ρUδt/(δx)です。その結果、要素圧力の対応する変化は下記によって与えられます。

(7) \displaystyle dp={{c}^{2}}d\rho =\frac{\rho {{c}^{2}}U\delta t}{\delta x}

各要素内の速度Uの摂動に応答する力は、式7による圧力変化と要素断面積δyδzの積です。したがって、ある要素の有効剛性kは、力を初期変位Uδtで除算したものです。

(8) \displaystyle k=\frac{\rho {{c}^{2}}U\delta t\delta y\delta z}{\delta xU\delta t}=\frac{\rho {{c}^{2}}\delta y\delta z}{\delta x}

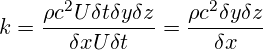
このkの値と式6によるMの定義を安定性条件の式5に代入することで、圧縮性流体の安定性条件が得られます。

(9) \displaystyle \frac{k\delta {{t}^{2}}}{M}={{\left( \frac{c\delta t}{\delta x} \right)}^{2}}\le 1

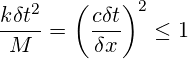
これは、1つの時間ステップ中に音波が進む距離を計算要素の幅よりも短く制限する、よく知られたクーラン条件です。シンプルな機械的モデルとの類似性によって、圧縮性流体中の音波の方程式を記述し、その方程式による安定性解析を実行する必要なしに、この結果が得られました。

粘性応力

粘度μの流体中の摂動速度Uに対して生成される粘性力は、x、yおよびz方向のせん断力で構成されます。たとえば、隣接するセル内の速度が0であると仮定すると、速度Uに対して要素の下面で作用するせん断応力はμU/δzです。要素の上面には圧縮応力が生じます。これらの応力のそれぞれは表面積δxδy (本例の場合)に作用し、粘性力を発生します。同様に、対応する面積に作用するxおよびy方向の応力も存在します。各方向において、(2つのばねと同様に)一組の力が存在しますが、式5のために1つのばねに対する有効剛性kを使用することが必要です。これは、すべての粘性力の合計を初期変位Uδtで除算したものの半分になります。

(10) \displaystyle k=\mu \left( \frac{U\delta y\delta z}{\delta x}+\frac{U\delta x\delta z}{\delta y}+\frac{U\delta x\delta y}{\delta z} \right)\frac{1}{U\delta t}

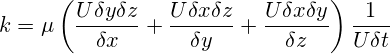
式5によって与えられる機械的モデルの安定条件にkのこの値を入れ、Mの式6を使用すると、下式が得られます。

(11) \displaystyle \frac{k\delta {{t}^{2}}}{M}=\frac{\mu }{\rho }\left( \frac{1}{\delta {{x}^{2}}}+\frac{1}{\delta {{y}^{2}}}+\frac{1}{\delta {{z}^{2}}} \right)\delta t\le 1

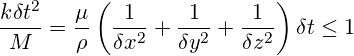
式11はオイラー格子で近似した陽的粘性応力の安定性条件です。

表面張力

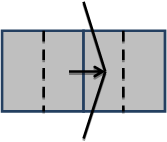
Figure 2A. With deformed interface.

図2A. 変形界面あり

図2Aに示すように、速度摂動Uによって変形している2個の要素の間に位置する流体界面を想定します。この例において、反作用は図2Aに示される表面の各区分に作用する表面張力による力です。簡単のために、2次元の表面(例: z方向の変化なし)と一定の表面張力係数を仮定します。

各区分内の表面張力は表面に沿う接線方向に作用するため、速度Uに対応する力は表面張力のx成分です。言い換えれば、垂直からの表面区分の角度の正弦を表面張力に乗算したものです。微小初期変位の場合、各表面区分からのx方向の力はσUδtδz/δyによって近似することが可能であり、その結果として下記の剛性係数が得られます。

(12) \displaystyle k=\left( \frac{\sigma U\delta t\delta z}{\delta y} \right)\frac{1}{U\delta t}

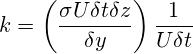
このkとMを式5に代入すると、表面張力に対する安定性条件が得られます。

(13) \displaystyle \frac{k\delta {{t}^{2}}}{M}=\frac{\sigma }{\rho }\frac{\delta {{t}^{2}}}{\delta x\delta {{y}^{2}}}\le 1

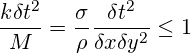
この結果は、δxとδyの指数が異なるため多少奇妙に見えますが、立方体または正方形要素の場合、その影響はありません。しかし、不均一な要素の場合は、yおよびz方向で同様の評価を行い、最も限定的な結果を使用することが必要です。いずれにしても、これは作用と反作用の原理に基づく非常にシンプルなモデルによる妥当かつ有益な結果です。

体積弾性

弾性特性を持つ流体の場合、速度Uの摂動は、ばねと非常によく似ている形式の弾性応力によって制限されます。流体の体積弾性率がεの場合、要素内の引張または圧縮に関連する応力はεUδt/δxとなります。この応力は表面積δyδzに作用し、剛性kはこの力を変位Uδtで除算したものです。これを式5に代入すると、下記の安定性条件が得られます。

(14) \displaystyle \frac{k\delta {{t}^{2}}}{M}=\frac{\varepsilon }{\rho }\frac{\delta {{t}^{2}}}{\delta {{x}^{2}}}\le 1

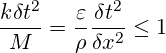
同様の結果がyおよびz方向にも存在します。

まとめ

シンプルな機械的モデルを使用して、作用と反作用の過程から生じる一般的なタイプの数値不安定性について説明しました。このシンプルなモデルを使用することで、オイラー格子での陽的有限差分近似によってモデル化された流体力学的な力に対するさまざまな安定性条件を迅速に導出することが可能です。これらの安定性条件は、機械的モデルシステムにおける質量と力に類似する、流体内の質量と力の概念を用いて導出されます。重要な点は、到達した安定性条件が一般的なものであり、特定の有限差分近似に依存しないことです。さらに、これらの導出によって、不安定挙動を生じさせるメカニズムを理解する簡単な方法も提供されます。

ここで使用したアプローチは、他のタイプの物理的力(例: 電気的力、非慣性力など)に拡張することが可能であり、移流によって生じる運動量の変化を等価力の結果として考えられるとの類似性を用いることによって、移流過程ですら含めることが可能です。

さらに、たとえばより多くの次元効果を含めることで、剛性係数のより精緻な推定を追加し、安定性条件を強化することもできます。いずれにしても、ここでの目的は、大抵の場合、数値不安定性をシンプルな解析から理解できると示すことです。ここで提供された洞察が、よりロバストで正確な数値近似の開発につながることが期待されます。

^ back to top