計算安定性

計算安定性

微分方程式の数値近似において、不安定な挙動が見られることは珍しくありません。つまり、計算結果で指数関数的に増大し、ときには符号が頻繁に反転するといった、元の微分方程式の解と何ら関係しない特性が見られることがあります。こうした挙動を「計算不安定性」と呼びます。

計算不安定性と、ときに物理現象問題で見られる物理的不安定性とを見分けることが重要です。しかし、実際には、こうした不安定な挙動の違いは必ずしも明白ではありません。計算された解において、有限差分の（時間または空間）増分ステップごとに符号が反転する特性が見られる場合、この不安定性は、ほぼ間違いなく数値近似によるものと考えられます。一方では、時間進行に伴う符号の反転は、多くの場合、時間増分を小さくすることで解決できます。それに対して、空間増分に伴う符号の反転は、計算解像度の不足を示している可能性があります。これも、空間増分を小さくすることで、問題を取り除くことができる場合があります。

一般に、物理的ではない、計算による不安定性が生じるのを予測できる方法が望ましいでしょう。あいにく、そうした汎用的手法はまだ考案されていません。しかし、よく遭遇する計算不安定性の多くを回避するのに十分な指針となる解析手法はいくつか存在します。基本概念を示す本書では、こうした手法のいくつかについて説明します。

計算不安定性の簡単な例

ここでは、計算安定性の基本概念について説明するのに適した簡単な例を示します。以下に示す簡単な反応速度式について考えます。

(1) \frac{\delta Q}{dt} = -AQ

ここで、Q=Q0、t=0とすると、この式の厳密解は、指数関数的減衰Q=Q0exp(-At)です。

数値近似を得るために、一定ステップサイズδtに時間を離散化し、t=n δtとします(nは整数)。数値的に計算されるQの値は、厳密解と区別するために小文字のqで表し、指数nを用いてタイムステップを表します。これにより、Q(n δt)の近似はqnとなります。式1の有限差分近似は、以下のように記述できます。

(2) q^{n+1} -q^n = -A \delta tq^n

ここで、q0=Q0とすると、非常に簡潔であるため、式2の厳密解を得られます。

(3) q^n = \left( 1 - A \delta t \right)^n q_{0}

ここで着目すべきことは、Aδtの値が変化するに従って、値qnがnとともにどのように変化していくかという点です。値は、n乗される括弧内(1-Aδt)の値の大きさに依存します(図1)。

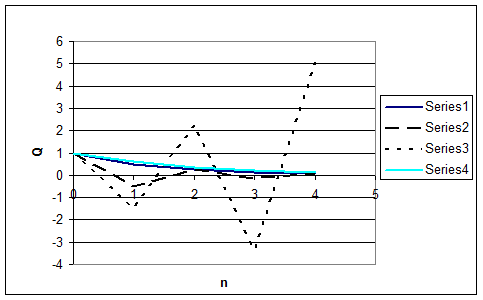
図1. 式3の値nにいくつかの値を代入した場合。シリーズ1はAδt=0.5、シリーズ2はAδt=1.5、シリーズ3はAδt=2.5、シリーズ4は式1から得た厳密値。

図1. 式3の値nにいくつかの値を代入した場合。シリーズ1はAδt=0.5、シリーズ2はAδt=1.5、シリーズ3はAδt=2.5、シリーズ4は式1から得た厳密値。

Aδtが2.0より大きいとき、括弧内は負となり、その絶対値は1.0より大きくなります。したがって、nが増大するたびにqnの符号は反転し、値は著しく増大していきます。これは、計算結果を見てもqがどのように変化していくかを把握できない計算不安定性が見られる典型的なケースです。これに対して、Aδtの値が1.0より小さいとき、括弧内は正となり、その絶対値は1.0より小さくなります。この場合、qnの変化は、近似値が厳密値をわずかに下回る、厳密解での指数関数的減衰の優れた近似となります。Aδtに中間的な値（1.0と2.0の間）を代入した場合、qn値は減衰しますが、タイムステップごとに符号が反転します。これらのことから、有限差分近似式2は、タイムステップδtが「安定条件」Aδt<1.0によって限定されるときに、厳密式に対して安定かつ妥当な近似を示すことがわかります。

von Neumannの線形安定性解析

20世紀における最も有名な数学者の一人であるJohn von Neumannは、現代のコンピュータの基礎を築いた功績者として知られていますが、有限差分方程式の特性を調べるための解析手法も開発しています。その手法は、差分方程式の計算安定性を評価するためにフーリエ級数を用いたアプローチをとるもので、参考文献1および2にその詳細が記述されています。

von Neumannのアプローチは、2つの仮定に基づいています。差分方程式は、解に含まれるわずかな摂動に対して線形化できること、そして、摂動に対する差分方程式内の項の係数を局所的に定数とみなすことができる、重なり合う領域セットが存在することです。これらの条件が満たされるとき、各領域でフーリエ級数を用いて摂動の局所的挙動を計算できます。

タイムステップnおよび空間内の離散位置jにおける摂動Pjnは、以下の形式をとるフーリエ項の総和として求まります。

(4) P_j^n \propto r^n e^{ikx}

ここで、xjはj番目の有限差分点の位置、kはモードの波数、rは時間振幅です。差分方程式の線形特性により、典型的なモードの挙動を考察するだけで済みます。典型的モードを線形化された差分方程式に代入することで、仮定された形式の解を得るために満たされるべき時間振幅rの代数方程式を得ます。これにより、ある範囲の波数にわたるフーリエモードの和から、摂動の完全解を得ることができます。

数値的に安定しているということは、時間が進行する(すなわち、nが増加する)に従って、各モードの大きさが制限なく増大してはならず、それはrの値の大きさが1以下でなければならないことを意味します。

線形安定性解析の例

von Neumannの手法を明確にするために、例を用いて説明します。ここでは、テストケースに適している移流拡散方程式を例にとります。

(5) \frac{\partial u}{\partial t} + c \frac{\partial u}{\partial x} = \nu \frac{\partial^2 u}{\partial x^2}

これは、関数u(x,t)の対流と拡散を表す式です。対流速度cおよび拡散係数νは定数です。この方程式の解は、良好な挙動を示すことがわかっています(つまり、物理的に安定している)。

定数であるタイムステップδtおよび空間ステップδxを用いてujn= u(jδx,nδt)とした、以下の簡潔な有限差分近似式を得ます。

(6) \frac{u_j^{n+1} - u_j^n}{\delta t} = - \frac{c}{2\delta x} \left(u_{j+1}^n - u_{j-1}^n \right) + \frac{\nu}{\delta x^2} \left(u_{j+1}^n - 2u_j^n + u_{j-1}^n \right)

この式にvon Neumannのモード式4を代入し、xj=jδxとして、rについて解きます。

(7) r=1-\left( \frac{ic \delta t}{\delta x} \right)\sin \left( k\delta x \right)-\left( \frac{2\nu \delta t}{\delta {{x}^{2}}} \right)\left[ 1-\cos \left( k\delta x \right) \right]

この式には実数項と虚数項が含まれており、rの絶対値の2乗は実数部と虚数部をそれぞれ2乗した和から求まります。

(8) {{r}^{2}}={{\left( 1-\frac{2\nu \delta t}{\delta {{x}^{2}}}\left( 1-\cos \left( k\delta x \right) \right) \right)}^{2}}+{{\left( \frac{c\delta t}{\delta x}\sin \left( k\delta x \right) \right)}^{2}}

この結果、式4の形式で解が非有界であってはならないという必要条件、すなわちrを1.0以下とする条件を満たすようなν、c、δtに対する制限が決定されます。

基本的に、rが極値となるのは、sinおよびcosの因数がそれぞれの極値である0.0、1.0、または-1.0のときです。たとえば、kδx=0のとき、r=1となります。このモードは中立安定であり、nの増加に伴う値の増大/減少はありません(すなわち、rn=1)。kδx=πのとき、r2の値は(1-4νδt/δx2)2となり、以下の安定条件が導き出されます。

(9) \frac{2\nu \delta t}{\delta {{x}^{2}}}\le 1

さらに、kδx=π/2のとき、安定条件r2<1は以下のようになります。

(10) {{r}^{2}}={{\left( 1-\frac{2\nu \delta t}{\delta {{x}^{2}}} \right)}^{2}}+{{\left( \frac{c\delta t}{\delta x} \right)}^{2}}\le 1

不等式の左辺は2乗の和であるため、どちらかの項が1を超えると左辺が1.0を超えることになり、安定解を得るための2つの条件が導かれます。

(11) \frac{c\delta t}{\delta x}\le 1 , \frac{2\nu \delta t}{\delta {{x}^{2}}}\le 2

1つ目の条件は新しい安定条件ですが、2つ目の条件については、より厳しい条件のものがすでに式9で示されています。これらの条件に加え、式10の第1項を展開して不等式を並べ替えることで求まる、もう1つの条件が与えられます。

(12) \frac{{{c}^{2}}\delta dt}{2\nu }\le 2-\frac{2\nu \delta t}{\delta {{x}^{2}}}

式9から、右辺の最小値は1.0です。これにより、拡散係数νの最小サイズに対する条件が与えられます。最終的に、満たすべき3つの安定条件が導かれます。

(13) \nu \ge \frac{{{c}^{2}}\delta t}{2} , \frac{c\delta t}{\delta x}\le 1 , \frac{2\nu \delta t}{\delta {{x}^{2}}}\le 1

これら3つの条件が満たされたとき、nが増加するに従ってフーリエモードが増大することはなく、制限のない不安定性が生じることはありません。特に、1つ目の条件は、十分な拡散がない限り、非ゼロの任意タイムステップに対して解が不安定になることを示している点で、非常に興味深いといえます。それに対して、残りの2つの条件は、最大タイムステップに対する単なる制限に過ぎません。

ここで、式13の1つ目の条件が満たされなかった場合、解は指数関数的に増大するだけですが、残りの2つの条件のどちらか一方でも満たされなかった場合には、指数関数的な増大だけでなく、時間増分ごとに符号が反転することに注目してください。この挙動をもたらす原因および有限差分方程式に関するその他の有用な情報については、安定性について説明する「CFD-101」の次の文書「ヒューリスティック解析」を参照してください。

このように、対象となる有限差分方程式が線形であり、重なり合う領域セット内で定数係数が用いられている場合には、von Neumannタイプのフーリエ解析が非常に有用であるといえます。より一般的な状況について計算安定性を解析する場合は、他の手法を考慮すべきです。

後注

指数や虚数に関する覚書として、von Neumannタイプの解析を実行する際に役立つと思われる恒等式を以下に挙げておきます。

\sin \theta =\frac{{{e}^{i\theta }}-{{e}^{-i\theta }}}{2i} , \cos \theta =\frac{{{e}^{i\theta }}+{{e}^{-i\theta }}}{2}

\sin \theta =2\sin \left( \frac{\theta }{2} \right)\cos \left( \frac{\theta }{2} \right) , \cos \theta ={{\cos }^{2}}\left( \frac{\theta }{2} \right)-{{\sin }^{2}}\left( \frac{\theta }{2} \right)

{{\sin }^{2}}\left( \frac{\theta }{2} \right)=\frac{1-\cos \theta }{2} , {{\cos }^{2}}\left( \frac{\theta }{2} \right)=\frac{1+\cos \theta }{2}

参考文献

  1. B.G. O’Brien、M.A. Hyman、S. Kaplan、『A Study of the Numerical Solution of Partial Differential Equations』、J. Math. Phys. 29、223 (1951)
  2. J. von Neumann、『Collected Works, IV』、Macmillan Co.、New York、NY (1963)

^ back to top