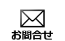長方形格子
長方形格子の拡張
数値流体力学の手法のほとんどは、空間を細分化して、流れ変数の平均値を定義できる離散化された体積要素の格子にすることに依存しています。最も単純な格子は、各座標軸(x、y、z)に垂直な一連の平面によって定義される長方形要素で構成されているものです。平行する平面間の間隔は、一定の場合と可変の場合があります。多くの場合、前者を「均一」長方形格子と呼び、後者を「不均一」長方形格子と呼びます。
長方形格子がシンプルな理由
長方形格子がシンプルなのは、非常に簡単に生成できるからです。必要なのは、座標方向ごとに、また、モデル化対象の空間を細分化している平面の合間で、格子の開始座標と終了座標を定義することだけです。
長方形格子の長所と短所
どんな格子生成システムでも同様ですが、対処が必要な長所と短所があります(「フリーグリッディングで時間を節約」を参照)。長方形格子の長所の1つは、格子を説明するために保存する情報量を最小限に抑えられることです。短所は、モデル化対象の領域が、長方形領域に収まらない場合があることです。たとえば、曲がりくねった川の鳥瞰図について考えると、長方形領域で設定した場合、長方形のほんの一部分のみを占めることになる場合があります。このような場合は、格子のほとんどの要素が川の外側に存在し、計算上負担になります。
差分方程式がシンプル
長方形格子のもう1つの長所は、一般的に長方形以外の格子に比べて差分方程式がシンプルであることです。たとえば、3次元では、ある要素内の速度に関するナビエストークス方程式の近似に必要なのは、隣接する6個の要素、つまり、3方向の座標1つにつき2つの隣接要素だけです。これに対して、長方形以外の格子の場合は、中心要素を囲む3x3x3=27の配列にあるすべての周辺要素に結合する必要があります。
数値的精度は格子要素が均一なときが最適な状態
一般的に、格子要素が均一なときに、有限差分方程式に関連付けられている数値的精度が最適な状態になります。これは、偏微分方程式の数値近似には、定義によって、物理量の空間的および一時的な値の変化率が関係してくるからです。1つの要素の両側の量の間で値の変化を評価する場合、要素が均一なときに最も精度が高くなります。これは、高次項は通常、対称によって相殺されるからです。不均一格子要素を使用する場合、精度を保つためには、通常はより複雑な数値近似が必要です(例については付録を参照)。
長方形格子の長所と短所の比較検討
長所と短所を比較検討することにより、シンプルな長方形格子には優れた特性が多数あることがわかるでしょう。ただし、複雑な幾何形状に対応するために課されている制限により、有用性が限定される場合があります。本書の残りの部分では、優れた特性を犠牲にすることなく長方形格子の有用性を大幅に拡大するための、概念的にシンプルな技法をいくつか説明します。わかりやすくするために、2次元の場合のみを説明しますが、3次元への拡張もごく簡単です。
長方形格子の表記法
長方形(2D)格子では、要素には通常、xとyの座標方向に対してそれぞれ整数iとjのラベルが付けられます。要素(i,j)の主要隣接要素は(i-1,j)、(i+1,j)、(i,j-1)、(i,j+1)です。セル内の物理特性は、2次元配列の値として保存されます。たとえば、要素(i,j)の圧力はp(i,j)となります。差分方程式をプログラミングするとき、インデックス付き配列を繰り返し使用する場合は、これらの量のメモリの場所を求めるために、算術演算としてi+1やj-1のようなインデックスシフトをコンパイラで実行する必要があります。
計算時間を短縮するために、複数インデックス付きの量を単一インデックス付きの配列に置き換えると便利です。複数の配列の場所は、一連の計算の最初に1回だけ計算されます。たとえば、ipj=i+1,jやijm=i,j-1などの表記は、短く、シンプルで、読み取りが簡単な単一インデックスです。これらは、ipがiプラス1を意味し、jmがjマイナス1を意味することなどを覚えておけば、簡単に読み取り可能です。このように、二重インデックス付きの量P(i+1,j-1)は、単一インデックス付きの量P(ipjm)に置き換えられ、その他も同様になります。この表記法は、使いやすく、計算時間を短縮できるだけでなく、以下に示すように、他にも非常に便利な特性を持っています。
複数の格子ブロック
長方形格子の有用性を拡張するための良い方法は、境界で結合されている複数の長方形格子を使用することです。図1Aと図1Bに示すように、シンプルな方法が2つ考えられます。連結ブロックは、ブロックが互いに隣接する境界の条件によって結合されます。入れ子ブロックは、互いに重ね合わされ、境界条件を使用して、入れ子側のブロックが外側のブロックに結合されます。
図1. (A)連結メッシュブロックと(B)入れ子メッシュブロック
最もシンプルなケースでは、ブロック境界の格子の線がすべて揃っていますが、重なり合う要素を補間法を使用して結合する場合は、その必要はありません。このタイプの格子強化のメリットは、数値ソルバのルーチンが、単一格子ブロックに使用されているものと同じであることです。ブロックを結合する境界条件だけは新しいため、個々のブロックに結合されているデータは、ブロック間を行き来するときに更新する必要があります。これらの要件はいずれも、単一ブロックの基本的なソルバアルゴリズムに追加できます。
このマルチブロック機能により、長方形格子の有用性は大きく拡大します。連結ブロック機能により、より広範囲の幾何形状領域を、より少ない格子要素でモデル化できるようになるからです。入れ子ブロック機能は、シミュレーションの解像度を局所的に高めるのに非常に便利です。高いコストをかけて、全領域に渡って高い解像度でシミュレーションする必要はありません。
分散メモリ並列化
マルチブロック機能を使用すると、分散メモリ並列化のための領域分割を自然な方法で行うこともできます。その後、ブロック間の境界で計算データを更新するには、クラスタの計算ノード間で、相互接続を使用して、そのデータを交換する必要があります。
非構造格子ブロック
さらに一般化を行うことにより、複雑な幾何形状領域の格子生成の効率を大幅に向上することができます。要素をシンプルな長方形で並べたものを、どの要素が隣接し合っているかを定義するリストに置き換えれば、不要な要素はすべて格子から排除できます。これによってメモリが解放され、ソルバルーチンは有効な格子要素のリストに従うだけになるため、計算時間はさらに短縮されます。このような「非構造」格子の簡単な図解を、図2に示します。

図2. 非構造長方形の例
構造化長方形格子では、隣接する要素のメモリの場所を簡単に計算できますが、それから非構造の要素に変更することは、一見困難な作業に思われるかもしれません。しかし、前述した単一インデックス表記法を使用すれば、たとえば(i, j+1)という場所がijpに置き換えられるため、非常に簡単に移行することができます。必要なことは隣接する要素のリストを使用して単一インデックス付きの値を再定義することだけです。そうすれば、ソルバのアルゴリズムやルーチンすべてを、それ以上の変更なしで使用できます。
どの非構造格子でも同様ですが、隣接セルのインデックスやその他のメッシュ関連の量を短時間で見つけられるようにするには、追加のストレージが必要です。構造格子と非構造格子の間の双方向マッピングを使用すると、大量のメモリリソースを使用することなく、非構造格子に効率的にナビゲーションできます。
この考え方のその他のバリエーションは、簡単に想像できます。たとえば、特定の要素に、物質が混在して含まれているため(流体と固体など)、複数の物理特性が必要な場合は、同じ場所で定義されている別の要素を要素リストに追加することができます。一致する要素は、混合要素の処理を目的とする特殊なリストで識別されます。
最もシンプルな格子システムのまとめ
最もシンプルな格子生成システムの進化的発展形と見なされるであろう長方形格子について、ここまで簡単に説明してきました。元のシンプルな格子システムの数あるメリットを維持しつつ、より高度なシミュレーションを求める声に応えるための手段として、いくつかの段階の比較的簡単な適応方法の概要が述べられています。
付録: 不均一格子の精度に関する図解
以下の説明は、『Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries』(C.W. Hirt、B.D. Nichols、J. Comp. Phys. 39、201 (1981))に基づいています。
不均一格子で発生する可能性のある問題について、非圧縮性流体の運動量の移流に関する項(発散形式では∇•uu)を数値近似することによって簡単に図解します。流体の一定密度は、この式から割り出されました。1つの幾何形状では、この項は以下のようになります。
![]()
ここでuは、x方向の流体速度です。通常は、運動量の保存を確実にするためのシンプルな方法である発散形式が望ましいでしょう。これは、図A1に点線で示した、2つの格子要素の間の境界にあるuの離散化された値に使用されているコントロールボリュームを検討することによって確認できます。2つの要素の間の境界に速度を配置することは、スタガード格子配列と呼ばれ、非圧縮性の流れモデルに多く使用されます。
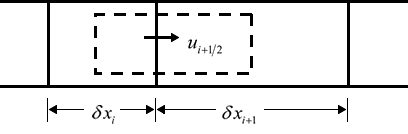
図A1. 要素の境界におけるu速度を差分近似するために使用される
コントロールボリューム(点線の長方形)
発散形式では、ガウスの定理を使用して、コントロールボリューム上部の移流フラックスの積算値を、その両側の境界フラックスに変換することができます。その後、コントロールボリュームを出たフラックスを、隣接するコントロールボリュームが自動的に獲得し、移流の際の運動量の保存が保証されます。
ただし、不均一格子での運動量の保存は、自動的に正確になるとは限りません。これを確認するには、上流つまりドナーの差分近似を使用して移流フラックスを近似すると仮定します(わかりやすくするために、uはすべて正の値とします)。これは、条件的に安定したアルゴリズムを提供することがわかっています。
![]()
ui+1/2という表記は、i番目の要素の右端に割り当てられている速度を表します。
この近似が元の偏微分方程式と「無矛盾」であることを確認するために、ここでは、u方程式が評価される場所x=xi+1/2に関するテイラー級数の差分方程式で、すべての項を展開します(CFD-101の記事の中の「ヒューリスティック解析」を参照)。
![]()
要素サイズが等しくない場合、明らかに、右辺はδx次まで左辺と一致しません。つまり、この差分近似は、元の微分式とゼロ次で一致しないため、「無矛盾」ではないということです。上流つまりドナー近似の代わりに、フラックス速度の中心値が使用されたとすると、近似は、均一格子の場合の2次ではなく、不均一格子で1次精度を有することにも注意してください。つまり、簡単な近似と思われるものが、均一格子の場合と比べて、不均一格子では1次分精度が下がるということです。
だからといって、不均一格子の精度が常に低いということにはなりません。局所化された領域では、流れの変数が最も急速に変化すると予測されるため、よりきめ細かいゾーン区分が可能になる場合があるからです。それでもやはり、不均一格子は注意して使用する必要があります。たとえば、要素サイズを緩やかに変化させることにより、近似次数の下げを最小限にするのがベストです。不均一格子でも精度が失われない、その他の近似法を探してもよいでしょう。これについては、移流項の保存形式の精度が低い理由が、u変数が配置されている位置に関してコントロールボリュームが中心に配置されていないことだということを観察する必要があります。近似の次数が1つ下がることを避けるためには、更新される変数の場所とそのコントロールボリュームの中心のずれを考慮して数値近似を修正しなければならなかったのです。